A Tale of Two Twins...
- Banadipa Chakraborty

- Sep 8, 2022
- 4 min read
Updated: Sep 9, 2022
Twins are always special. But they are more special in Special Theory of Relativity. Twins always create confusion by tricking us using their similar faces. They didn't even spare relativity. There is a whole paradox in the name of twins which turned many of the physicist's hair into white (if they weren't blonde). Here, we'll understand how the paradox arises and try to find a solution to this.
Before going into the paradox, I would like to discuss something which I encountered while studying Relativity. The Muon Decay Problem is common to all of us who studied relativity. So, how muons regularly travel through such a long distance without spontaneously decaying while they could only travel through a distance which is less than 1k.m. Most of us know it’s because of time dilation since it is travelling approximately close to the speed of light in vacuum (c). According to our perspective, they’ll reach the Earth’s surface and we could easily detect them with the help of a detector. But, what about the Muon’s perspective? It doesn’t know anything about time dilation, what it’ll basically see is that the Earth is moving towards it at a speed close to the speed of light (c) and so the length is contracted, so the distance traveled by muon is shortened.
Therefore, there arises a question which I thought for a while as to what exactly Reality is then. The same incident which is happening here has different versions in different frames. I would answer this question while explaining the Twin Paradox below.
Now, let us consider two twins: - Jane & Joe. Jane decides to travel in a spacecraft and Joe will stay here on Earth. They both agree to send a light beam after every one year to mark the completion of their anniversary of separation. When Joe sees Jane moving away from Earth, she’ll think that Jane would age slowly as Jane is moving and according to STR moving clocks run slow, while Jane will think that Joe will age slowly. As for her, she’ll see that she is at rest and the Earth is drifting away from her. So, both infer that the other one will be younger when they meet again. Here the paradox arises. Both can’t be true simultaneously.
Now, its resolution lies in the very fact that both the events are not symmetric, i.e., both Jane and Joe are not travelling for an infinite time (in their respective perspectives) they’ll meet again and this will mark the end of their journey.
Therefore, their respective observations will definitely converge into a single and same fact which I would like to explain with the help of a diagram.
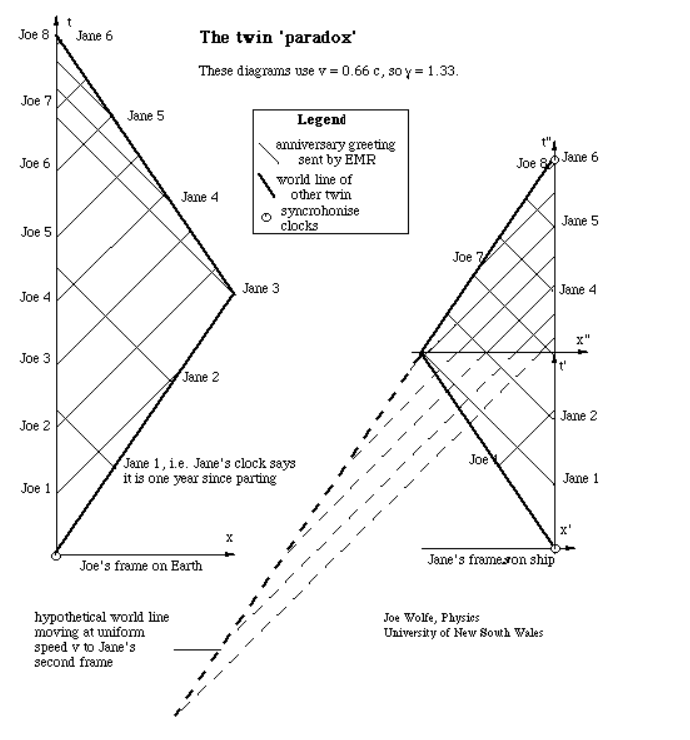
First, we consider Joe’s frame of reference. From her frame she sees that she is at rest and Jane is moving away in the initial phase of the journey.
Now, we see that during the initial half of the journey, Joe sends 4 signals while she receives only 2 signals from Jane. And, during the second phase of the journey when Jane is moving close to Earth, Joe sends another 4 signals while this time she receives 4 signals from Jane in a frequent manner.
Therefore, according to Joe her age increases by 8 years while Jane’s age by 6 years.
Now, considering Jane’s frame of reference. From her frame she sees that she is at rest while Joe is drifting away from her in the initial phase of the journey. During the initial phase, Jane sends 2 signals and ends up receiving only 1 signal. During the next phase of the journey when Joe is moving closer to Jane, Jane sends 4 signals while she receives 7 frequent signals.
Therefore, according to Jane her age increases by 6 years while Joe’s by 8 years, which is in context with the first scenario.
Here, we see that Joe’s assumption was correct. Infact, from the diagram we could easily rule out the possibility of a Paradox.
Now, coming back to my question of reality, observations which we see in our respective frames are completely frame dependent and this is what we perceive as reality. Since there is an asymmetry in the above paradox, both observations will converge to the same result, making only one of them correct.
To give a complete picture of the scenario we should also have to address a question which often remains unanswered, which is about the biological clock as how it’ll adjust itself in such cases.
To answer that, let us consider another example. Anaa and I are best friends, she lives in another galaxy. As it was my birthday, she decided to surprise me with a cake which she would bake in between the journey as it takes only one hour for her to visit me (from my reference frame) and also to bake a cake. So, she put the cake in the oven of her spaceship and left it to bake. When she finally reached here, I saw that her cake was still half-baked, although 1 hour had passed for me. When I saw her watch, it showed that only 20 minutes had passed for her, which is less than the approximate time for baking the cake.
Therefore, from this simple case, we see that the biological clock doesn’t adjust itself to the surroundings, rather it remains the same as it should be, if it had adjusted itself then the cake would have been perfectly baked. It happened because, from Anaa’s perspective she saw that the distance she needs to traverse is shortened which is similar to the case in Muon decay (in muon’s frame of reference).
"Our astronauts, when they go orbiting around the earth, they actually come back slightly younger than a twin that they would have on the planet Earth who was stationary. This is called the twin paradox." --Michio Kaku



Comments